For accurate statistical analysis of the 2dFGRS it is essential to fully understand the criteria that define the parent photometric catalogue and also the completeness of the redshift catalogue, as discussed in Colless et al. (2001) and Norberg et al. (2002). For this purpose we have defined maps or masks characterizing this information as a function of position on the sky:

1. The magnitude limit mask gives the extinction-corrected magnitude limit of the survey at each position.
2. The redshift completeness mask gives the fraction of measured redshifts at each position.
3. The mu-mask gives the dependence of the redshift completeness on apparent magnitude.

We now describe in more detail how these masks are defined and briefly outline some of their uses.

1. Magnitude limit mask

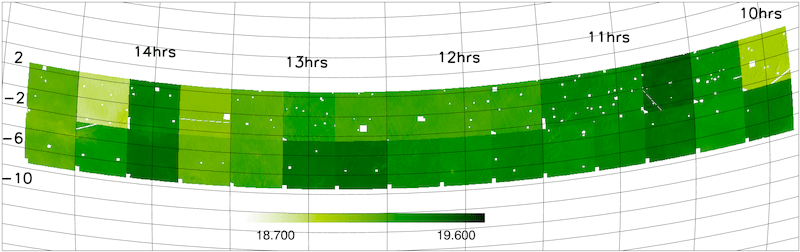
Although the 2dFGRS sample was originally selected to have a uniform extinction-corrected magnitude limit of b=19.45, in fact the survey magnitude limit varies slightly with position on the sky. There are two reasons for this. First, the photometric calibrations now available are much more extensive than when the parent 2dFGRS catalogue was originally defined. This has enabled us to recalibrate the whole 2dFGRS parent catalogue and results in improved zero-point offsets and linearity corrections for each of the UKST photographic plates. Second, the extinction corrections have been changed to use the final published version of the Schlegel et al. (1998) extinction maps; the original extinction corrections came from a preliminary version of those maps.

The magnitude limit mask is therefore defined by the change in the photometric calibration of each UKST photographic plate and the change in the dust extinction correction at each position on the sky. The magnitude limit masks for the NGP and SGP strips using the photometric calibration of the 2dFGRS Final Data Release are shown below in a zenithal equal area projection. Note that the masks also account for the holes in the source catalogue around bright stars and plate flaws.

In the SGP, which is a subset of the APM galaxy survey (Maddox et al. 1990a,b), the rms change in plate zero-point is only 0.03 mag. However, in the NGP region the original calibration was less accurate and the change in zero-points have an rms of 0.08 mag. The change in the dust corrections are also less in the SGP, as the extinction is generally lower in this region. In the SGP the rms magnitude change due to improved dust corrections is 0.01 mag while in the NGP it is 0.02 mag.

In the SGP the mean limiting magnitude is b=19.40 with an rms about this value of 0.08 mag; in the NGP the mean limiting magnitude is b=19.29 with an rms of 0.12 mag.

For accurate statistical analysis of the 2dF survey, the magnitude limits defined by this mask should be used. It is always possible to analyse the data with a fixed magnitude limit if one is prepared to omit both the areas of the survey that have magnitude limits brighter than the chosen limit and also all the galaxies in the remaining areas with magnitudes fainter than the chosen limit.

2. Simple redshift completeness mask

The best way to define a redshift completeness mask is to make use of the geometry defined by the complete set of 2 degree fields that were used to tile the survey region for spectroscopic observations. Each region of the sky inside the survey boundary is covered by at least one 2 degree field, but more often by several overlapping fields. We define a sector as the region delimited by a unique set of overlapping 2 degree fields. This is the most natural way of partitioning the sky, as it takes account of the geometry imposed by the pattern of 2 degree fields and the way in which the galaxies were targeted for spectroscopic observation. Within each sector, theta, we define the redshift completeness, R(theta), as the ratio of the number of galaxies for which redshifts have been obtained, N_z(theta), to the total number of objects contained in the parent catalogue, N_p(theta):

R(theta) = N_z(theta)/N_p(theta) .

The redshift completeness of a given sector, R(theta), should be clearly distinguished from the redshift completeness of a given field, C_F, since multiple overlapping fields can contribute to a single sector.

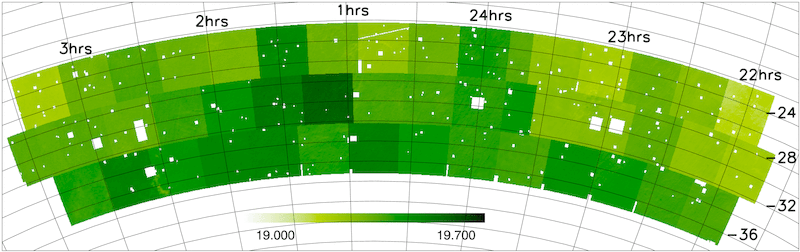
The redshift completeness masks for the 2dFGRS Final Data Release (where redshift completeness is defined as above) are shown below. The masks are plotted in a zenithal equal area projection.

These simple redshift completeness masks can be used to locate regions in which the redshift completeness is high. They can also be used as a first step in either applying weights to statistically correct for incompleteness or to construct random unclustered catalogues that have the same angular pattern of incompleteness as the redshift sample (for use in estimating correlation functions).

For this latter purpose, one should also take account of how the redshift completeness depends on position within a sector as a result of constraints on fibre positioning and other considerations. This is best done by using the parent catalogue to derive weights for each galaxy with a measured redshift (see Norberg et al. 2002).

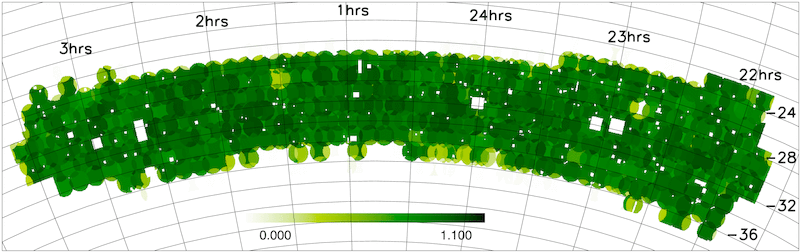
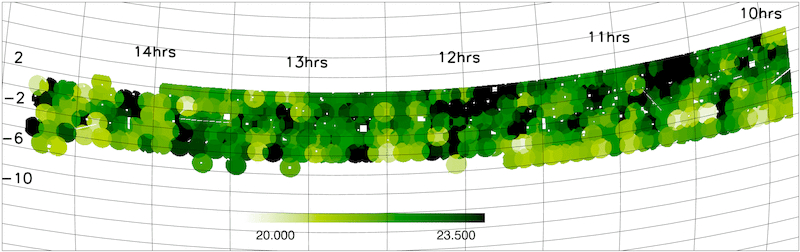
3. Magnitude-dependent completeness corrections (mu-mask)

For many applications one also needs to take account of how the redshift completeness depends on apparent magnitude, as discussed in detail in Colless et al. (2001) and Norberg et al. (2002). This requires knowing the mu parameter that characterises the fall-off in completeness with apparent magnitude for each sector.

Correction: In the definition of the magnitude-dependent completeness mask in section 8.3 of Colless et al. (2001), there is an error in the value given for the parameter alpha; the paper gives alpha=0.5, but the correct value is alpha=0.5ln(10).

The mu-masks for the 2dFGRS Final Data Release are shown below. The masks are plotted in a zenithal equal area projection.